在参加 P 国主办的 Pre-SDOI Training Camp(也被称作 Public Easy Round #2)时,你遇到了一道这样的题:
给定一个 n 个点 m 条边的有向图 G ,保证其基图 G′ 是仙人掌且没有重边自环。你需要求出有序点对 (x,y) 的个数,使得在 G 中存在一条从 x 到 y 的路径。特别地,(x,x) 也需要计入答案。
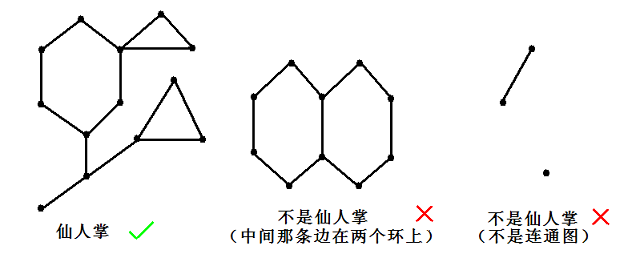
仙人掌的定义:一个连通的简单无向图,且每条边都在至多一个简单环内。
基图的定义:对于一个有向图 G=(V,E) ,定义一个新的无向图 G′=(V,E′) ,且 E′ 就是把 E 的每条有向边替换为无向边得到的边集。称 G′ 为 G 的基图。
输入格式
第一行,一个正整数 T ,表示数据组数,之后对于每组数据:
- 第一行两个正整数 n,m 。
- 接下来 m 行,每行两个正整数 u,v ,表示一条从 u 到 v 的有向边。
输出格式
对于每组数据:
- 一个非负整数,表示答案。
样例一
input
2 3 3 1 2 1 3 2 3 5 5 1 2 2 3 3 4 4 5 4 2
output
6 18
样例二
见下发文件。
数据范围与提示
对于所有数据,保证 1≤T≤105,2≤n≤2.5×105,n−1≤m≤⌊3(n−1)2⌋,∑n≤2.5×105 。
| 子任务编号 | 追加限制 | 分数 |
|---|---|---|
| 1 | n≤8,m≤10 | 4 |
| 2 | 96 |
时间限制:2s
空间限制:512MB