这是一道通信题。
P 国的国土可被视为一张 N 个点 M 条边的有向图,其中第 i (0≤i≤M−1) 条边的起点为 Ui,终点 Vi,长度为 Wi。顶点的编号均为 0∼N−1 中的正整数。
在【PER #2】情报传递中,你(Participant)通过内鬼的指引,成功得到了 Public Easy Round #2 的比赛地点。为了避免类似的情况再次发生,P 国下令决定下一场比赛的比赛流程将分为 Q 天。对于每个 0≤i≤Q−1,第 i 场考试将要求所有考生必须统一到达顶点 Si 处,随后才能够前往考试地点 Ti。
你已经提前得知了 P 国的地图与接下来 Q 场考试的 S0,S1,⋯,SQ−1 与 T0,T1,⋯,TQ−1。你希望对每个 0≤i≤Q−1,计算出从顶点 Si 道顶点 Ti 的最短路径,以备规划考试时的行走路线。
不幸的是,由于通信传输的故障,你所得到的地图中,有恰好 K 条边 E0,E1,⋯,EK−1 的长度发送失败了。好在你发现,这些发送失败的边的起点均相同,即 UE0,UE1,UE2,⋯,UEK−1 的值均相等。
你通过随身携带的通讯设备,向内鬼 Spy 发送了你丢失长度的边的编号 E0,E1,⋯,EK−1。随后,内鬼 Spy 可以向你发送一个长度不超过 1000 的 0/1 串,你需要根据这些信息,求出每个 Si 到 Ti 的最短路径。
实现细节
这是一道通信题,本题仅支持 C++ 语言。
你需要提交两个程序,其中程序 Spy 描述内鬼向你发送信息的策略,程序 Participant 描述你的策略。
Spy
你需要包含头文件 Spy.h,并实现以下函数:
std::string SpySolve(int N, int M, int Q, int K, std::vector <int> U, std::vector <int> V, std::vector <long long> W,
std::vector <int> S, std::vector <int> T, std::vector <int> E);- 在每个测试点中,该函数会被调用恰好一次。
- 参数 N 表示顶点的数量 N。
- 参数 M 表示有向边的数量 M。
- 参数 Q 表示比赛的天数 Q。
- 参数 K 表示丢失长度的边的数量 K。
- 参数 U 为一个长为 M 的数组 U0,U1,⋯,UM−1,描述每条边的起点。
- 参数 V 为一个长为 M 的数组 V0,V1,⋯,VM−1,描述每条边的终点。
- 参数 W 为一个长为 M 的数组 W0,W1,⋯,WM−1,描述每条边的长度。
- 参数 S 为一个长为 Q 的数组 S0,S1,⋯,SQ−1,描述每组询问的起点。
- 参数 T 为一个长为 Q 的数组 T0,T1,⋯,TQ−1,描述每组询问的终点。
- 参数 E 为一个长为 K 的数组 E0,E1,⋯,EK−1,描述被丢失的边的编号。
- 你需要返回一个仅包含
0与1的字符串 Z,描述 Spy 需要发送给 Participant 的信息。
Participant
你需要包含头文件 Participant.h,并实现以下函数:
void ParticipantSolve(int N, int M, int Q, int K, std::vector <int> U, std::vector <int> V, std::vector <long long> W,
std::vector <int> S, std::vector <int> T, std::vector <int> E, std::string Z);- 在每个测试点中,该函数会被调用恰好一次。
- 参数 N 表示顶点的数量 N。
- 参数 M 表示有向边的数量 M。
- 参数 Q 表示比赛的天数 Q。
- 参数 K 表示丢失长度的边的数量 K。
- 参数 U 为一个长为 M 的数组 U0,U1,⋯,UM−1,描述每条边的起点。
- 参数 V 为一个长为 M 的数组 V0,V1,⋯,VM−1,描述每条边的终点。
- 参数 W 为一个长为 M 的数组 W0,W1,⋯,WM−1,描述每条边的长度。特别地,对于所有 0≤i≤K−1,都有 WEi=−1,表示这些边的长度信息已经丢失。
- 参数 S 为一个长为 Q 的数组 S0,S1,⋯,SQ−1,描述每组询问的起点。
- 参数 T 为一个长为 Q 的数组 T0,T1,⋯,TQ−1,描述每组询问的终点。
- 参数 E 为一个长为 K 的数组 E0,E1,⋯,EK−1,描述被丢失的边的编号。
- 参数 Z 表示 Spy 发送给 Participant 的
0/1串 Z。
你需要调用以下函数恰好 Q 次:
void Report(std::vector<int> P);- 在每个测试点中,你需要调用该函数恰好 Q 次。
- 对于第 i 次调用(0≤i<Q),参数 P 需要描述第 i 组询问的最短路径。
- 设 P 的长度为 L,则你需要保证 AP0=Si,BPL−1=Ti,且对任意 0≤k≤L−2,都有 BPk=APk+1。
- 换句话说,P 按顺序描述了路径上每条边的编号。
- 你可以提交任意一组合法的最短路径。
样例交互库
本题下发文件中含有样例交互库 grader.cpp,选手可使用以下命令编译得到可执行文件:
g++ Participant.cpp Spy.cpp grader.cpp -o answer -O2
可执行文件将从标准输入中通过以下格式读取输入数据:
- 输入的第一行包含四个整数 N,M,Q,K。
- 接下来 M 行,每行三个整数 Ui,Vi,Wi。
- 接下来 Q 行,每行两个整数 Si,Ti。
- 接下来 K 行,每行一个整数 Ei。
可执行文件将向标准输出中输出以下数据:
- 若通信过程出现了错误,则输出对应的错误信息。
- 否则,输出将包含恰好 Q 行。
- 每行首先包含一个整数 k,表示路径的长度。
- 接下来 k 个整数,描述路径。
需要注意的是,样例交互库并不会检查你的答案是否正确。为了提高大家的参赛体验,在下发文件中提供了样例校验器 checker.cpp。选手可以使用以下命令编译得到可执行文件 checker:
g++ checker.cpp -o checker -O2 -std=c++14
随后,你可以使用以下命令来检查你的程序:
./checker <input-file> <output-file>
其中 input-file 为你想要检查的测试用例的输入文件,output-file 为你想要检查的测试用例的输出文件。
需要注意的是,在最终评测时,所使用的交互库与下发的样例交互库有所不同。特别地,程序 Spy 与 Participant 将分别编译并运行在两个不同的进程中,两个进程之间不能通过任何方式进行通信。选手程序不应该也不能从标准输入中读取任何信息,或向标准输出中输出任何信息,否则可能会产生不可预料的错误。
本题的时间限制与空间限制均指进程 Spy 与 Participant 各自的限制,即你需要保证两个进程均不超过时间限制(1.0 秒)与空间限制(512MB)。保证在最终使用的两个交互库中,每个交互库所消耗的时间均不超过 50ms,空间均不超过 8MB,即每个进程都至少有 950ms 的时间与 504MB 的空间可用。
样例数据
样例 1 输入
5 5 3 1
0 1 2
0 2 3
0 3 1
1 4 5
2 4 5
0 4
1 4
0 3
1样例 1 输出
2 0 3
1 3
1 2样例 1 解释
本组数据中的有向图如下所示:
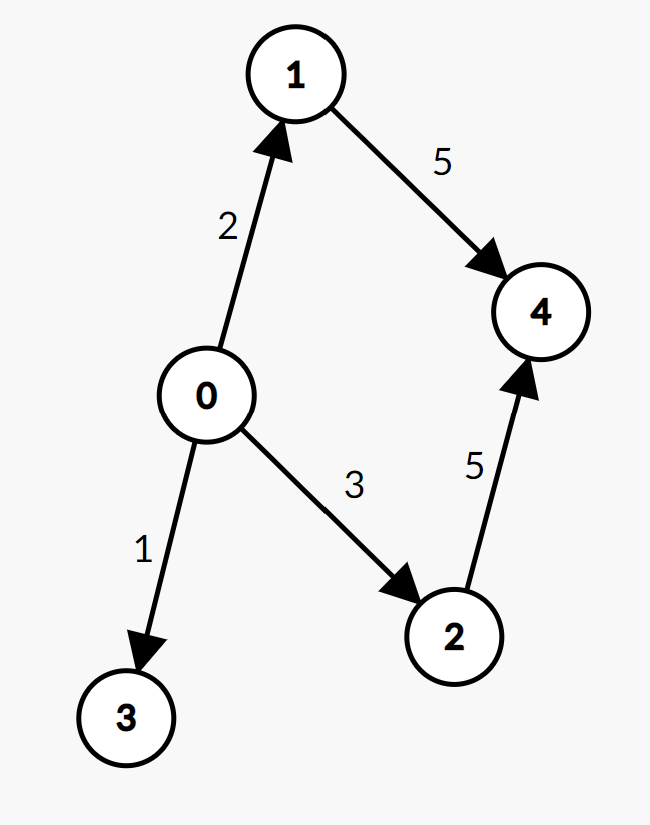
对于第一组询问,最优的路径为 0e0⟶1e3⟶4,路径的长度为 7。
对于第二组询问,最优的路径为 1e3⟶4,路径的长度为 5。
对于第三组询问,最优的路径为 0e2⟶3,路径的长度为 1。
故程序 Participant 应当依次调用以下函数:
Report({ 0, 3 });Report({ 3 });Report({ 2 });
样例 2 输入
6 7 4 3
0 1 2
0 2 4
0 5 3
1 3 3
1 4 2
2 1 1
4 2 1
0 3
0 4
4 3
2 1
0
1
2样例 2 输出
2 0 3
2 0 4
3 6 5 3
1 5子任务
对于 100% 的数据,2≤N≤300,1≤M≤N×(N−1),1≤Q≤60,1≤K≤5,0≤Ui,Vi,Si,Ti≤N−1,1≤Wi≤1016,0≤Ei≤M−1。
对于 100% 的数据,图中不存在重边与自环(即 (Ai,Bi) 两两不同,且 Ai≠Bi),不存在重复的询问(即 (Si,Ti) 两两不同),询问的起点与终点不同(即 Si≠Ti),且 E0,E1,⋯,EK−1 两两不同。
对于 100% 的数据,保证从 Si 到 Ti 至少有一条合法的路径,保证 UE0=UE1=UE2=⋯=UEK−1。
设 Y 表示 Spy 能够返回的 0/1 串的最长的长度,L 表示你所返回的 0/1 串的长度。
| 子任务编号 | Q≤ | Y= | 特殊性质 | 分值 |
|---|---|---|---|---|
| 1 | 10 | 1000 | A | 5 |
| 2 | 60 | 180 | 无 | 95 |
- 性质 A:保证存在一条从 Si 到 Ti 的最短路径,使得所经过的边的数量不超过 10。
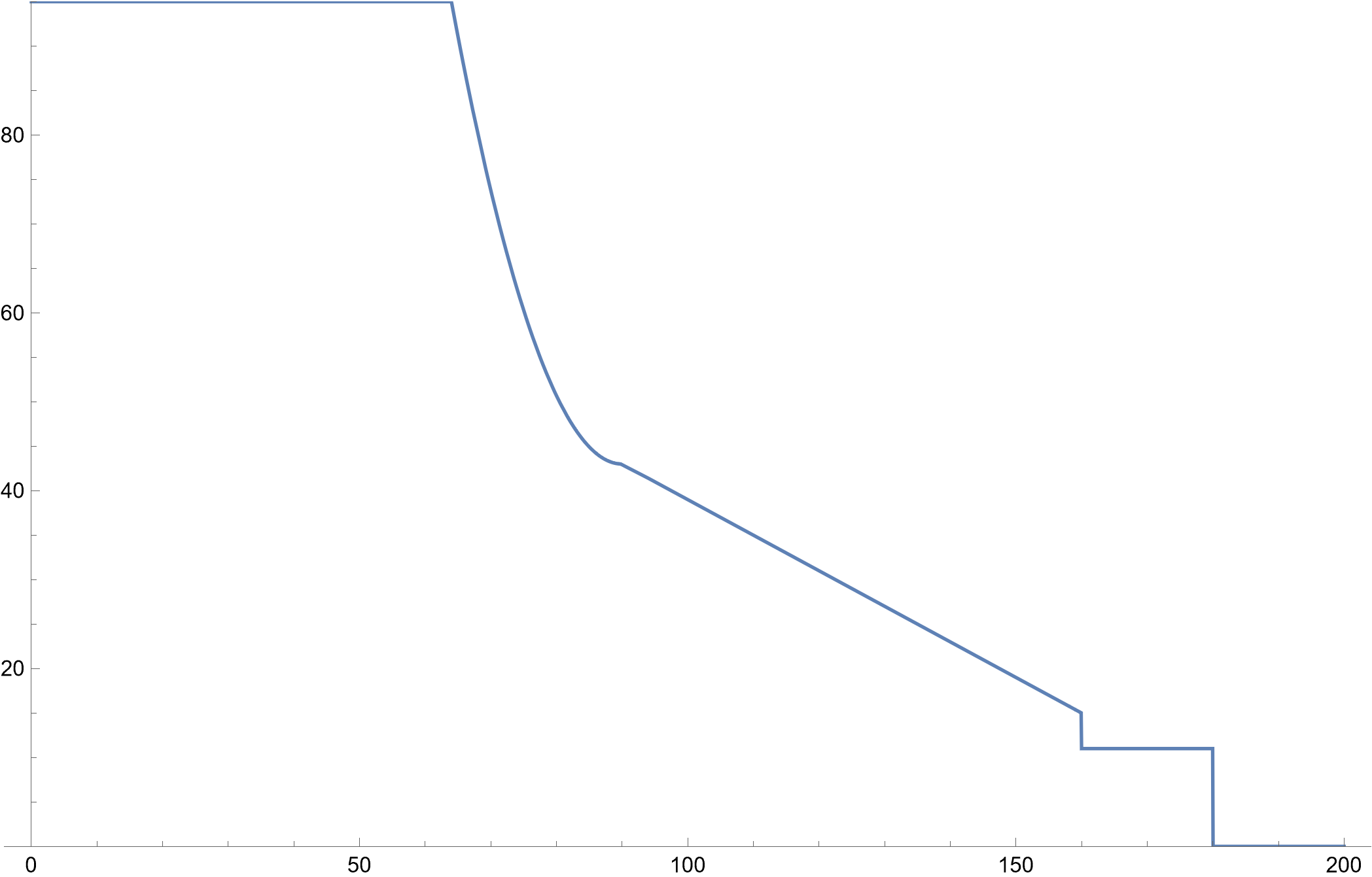
对于子任务 2,你的得分将于 L 的值有关:
| L | 分值 |
|---|---|
| 180<L | 0 |
| 160<L≤180 | 11 |
| 90<L≤160 | 15+2(160−L)5 |
| 64<L≤90 | 43+52⋅(90−L90−64)2 |
| L≤64 | 95 |