给定 n 与一个长度为 n+1 的整数序列 a0,a1,⋯,an。
有这样一个分段函数 f(x),其定义域为 [0,n],且 f(x) 的值为:
- 若 x 为一个整数,则 f(x)=ax。
- 否则,记 k=⌊x⌋,则 f(x)=ak+(x−k)(ak+1−ak)。
现在,两名玩家 Min 与 Max 将进行以下游戏,在游戏前,双方商定了一正整数 A 与一正实数 ε,并记参数 T=A。
随后,Max 将选择一实数 x∈[0,n],游戏正式开始。双方将轮流对 x 进行修改,且由 Min 首先进行,规则如下:
- 若 T≤0,游戏立刻结束。
- 该方玩家选择另一实数 x′ 满足 x′∈[0,n],且 |x−x′|<T。
- 将 x 修改为 x′,并将 T 修改为 T−ε。
显然,对任意 ε>0,游戏都将在有限多轮后结束。Min 希望最小化游戏结束后 f(x) 的值,而 Max 希望最大化游戏结束后 f(x) 的值。记 R(A,ε) 表示如果事先选择的参数分别为 A,ε,则最终 f(x) 的值将会是多少。则给定 A 你需要计算:
lim
输入格式
本题的每个测试点中可能包含多组测试数据。
输入的第一行包含一个整数 T,表示数据组数。
对于每组数据:
输入的第一行包含两个整数 n, A。
接下来一行,包含 n+1 个整数 a_0, a_1, \cdots, a_n.
输出格式
输出一行一个实数,表示答案。你与答案的误差不能超过 10^{-4}。
形式化地,设你输出的答案为 A_p,正确的答案为 A_j,则当且仅当 \displaystyle \frac{|A_p - A_j|}{\max(1, |A_j|)} \le 10^{-4} 时,会判定你的答案正确。
样例数据
样例输入
2
3 1
11 -4 -5 14
6 4
2 5 4 6 -1 5 -10样例 1 输出
4.5
4.4705882352941176470588235294118样例解释
对于第一组测试数据,下图为 f(x) 的图像。
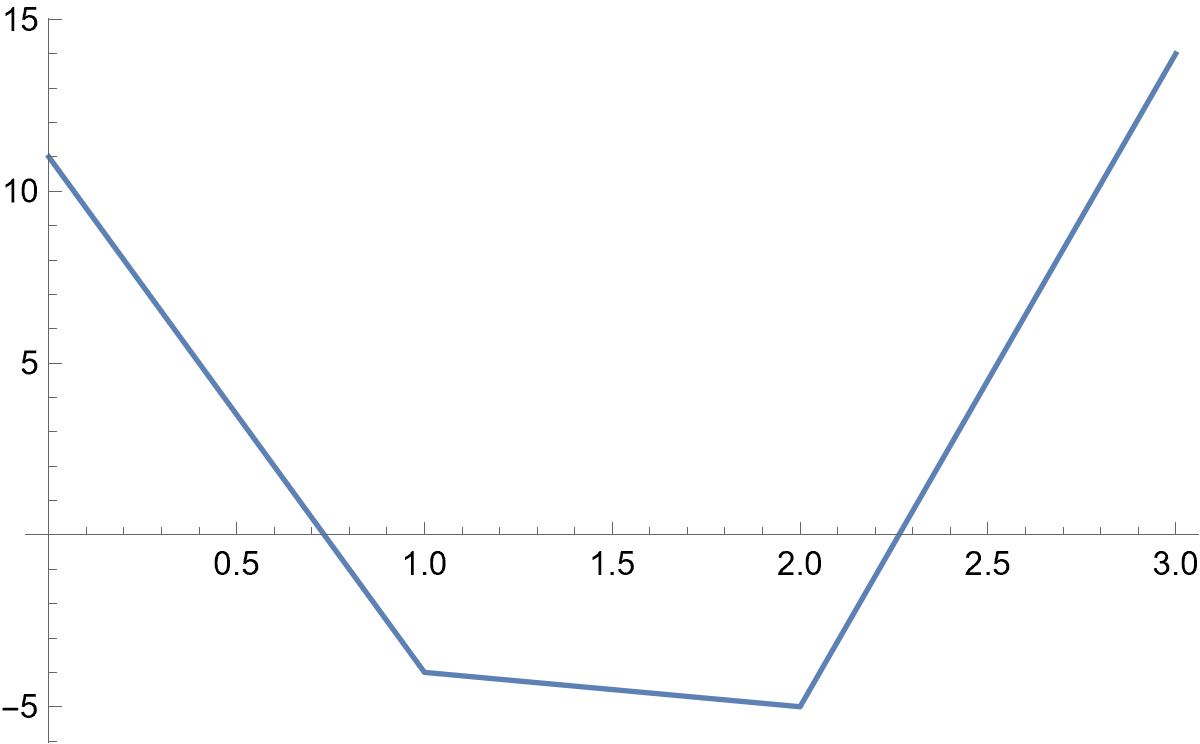
真实的答案为 \displaystyle\frac{9}{2}。
对于第二组测试数据,真实的答案为 \displaystyle \frac{76}{17}。
子任务
对于所有数据,1 \le A \le n \le 10^5,1 \le \sum n \le 10^5,-10^6 \le a_i \le 10^6。
| 子任务编号 | n \le | A | 分值 |
|---|---|---|---|
| 1 | 1 | 不保证 | 3 |
| 2 | 2 | 5 | |
| 3 | 3 | 7 | |
| 4 | 5 | 14 | |
| 5 | 14 | 12 | |
| 6 | 80 | 12 | |
| 7 | 1\,000 | 12 | |
| 8 | 10^5 | A = 1 | 10 |
| 9 | 不保证 | 25 |